变相同一法

变相同一法指的是：

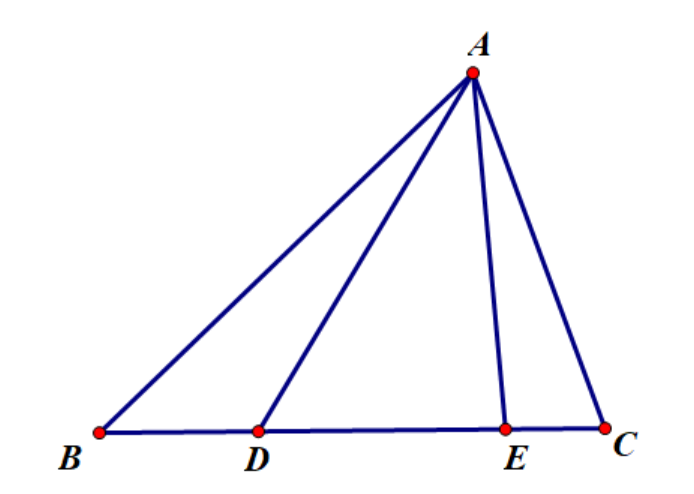
如图，则有
$$\angle BAD =\angle CAE \Leftrightarrow \dfrac{\sin \angle B A D}{\sin \angle D A C}=\dfrac{\sin \angle C A E}{\sin \angle E A B}. $$

---

定理之证明

证明：只需证明充分性即可.

化为三角形式即：$$ 0<\alpha,\beta<\theta<\pi,\dfrac{\sin(\theta-\alpha)}{\sin \alpha}=\dfrac{\sin(\theta-\beta)}{\sin \beta} \Rightarrow \alpha=\beta. $$

利用积化和差有：$$ \Leftrightarrow\cos(\theta-\alpha-\beta)-\cos(\theta-\alpha+\beta)=\cos(\theta-\alpha-\beta)-\cos(\theta-\beta+\alpha) $$ $$ \Leftrightarrow\sin \theta \sin(\beta-\alpha)=0 $$

由\(\theta\)范围知\(\sin \theta \neq 0\)，故\(\beta=\alpha\)，得证.

\(\Box\)

---

利用变相同一法即可将角相等的证明转化为三角式的比例关系，从而可以利用分角定理等进行进一步处理。