奠基性的正弦定理
约 600 个字 4 张图片 预计阅读时间 3 分钟
正弦定理:
对\(\triangle ABC\),有 \(\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}=2R\).
定理之证明
证明是简单的,左边两个等号只需要注意到 \(a\sin B=b\sin A=c\)上的高,而最后一个等号需要用到三角形外接圆以及圆周角相等.
正弦定理的奠基性在于它定量地刻画了三角形的一个概念:大边对大角,也定量地刻画了三角形的边和角的关系,使得它可以作为一系列基本定理的证明工具。
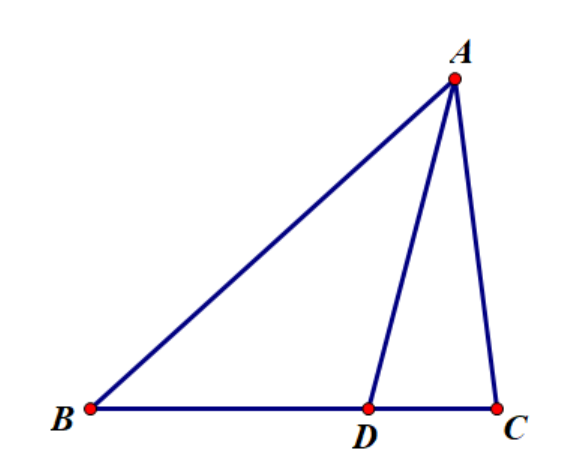
如图,\(\triangle ABC\)及\(BC\)边上一点\(D\),有\(\dfrac{S_{\triangle ABD}}{S_{\triangle ADC}}=\dfrac{BD}{DC}\).
定理之证明
证明:利用正弦定理与面积公式\(S_{\triangle ABC}=\frac{1}{2}ab\sin C\)得:
\(\dfrac{S_{\triangle ABD}}{S_{\triangle ADC}}=\dfrac{c\times BD\sin B}{b\times DC\sin C}=\dfrac{BD}{DC}\). 得证。


如图,\(\triangle ABC\)及\(BC\)边上一点\(D\),有\(\dfrac{BD}{DC}=\dfrac{AB\sin\angle BAD}{AC\sin\angle DAC}\).
定理之证明
证明:利用借助正弦定理证明的共边比例定理以及面积公式\(S_{\triangle ABC}=\frac{1}{2}ab\sin C\)得:
\(\dfrac{BD}{DC}=\dfrac{S_{\triangle ABD}}{S_{\triangle ADC}}=\dfrac{\frac12 AB\times AD\sin\angle BAD}{\frac12 AD\times AC\sin\angle DAC}=\dfrac{AB\sin\angle BAD}{AC\sin\angle DAC}\). 得证。
比例的写法
这里我们采用了\(\dfrac{BD}{DC}\),\(\dfrac{\sin\angle BAD}{\sin\angle DAC}\),\(\dfrac{S_{\triangle ABD}}{S_{\triangle ADC}}\)的写法,是有讲究的,具体如下:
- \(\dfrac{BD}{DC}\)为形如 (始点(\(B\))\(\rightarrow\)分点(\(D\)))/(分点(\(D\))\(\rightarrow\)终点(\(C\))) 的比例写法,在后续定理中也会多次体现,这样书写“分比”有利于我们书写比例。
- \(\dfrac{\sin\angle BAD}{\sin\angle DAC}\)也类似于起边 \(\rightarrow\) 分边 \(\rightarrow\) 终边的写法,但是一般我们用有向角解释:
有向角:以\(AB\)为始边,\(AC\)为终边的角记为\(\measuredangle BAC\),逆时针角的大小为正,顺时针为负。
由于有向角的存在,我们希望角度的起点 \(\rightarrow\) 顶点 \(\rightarrow\) 终点满足逆时针,这样分数线上下的角能够保持同号. - \(\dfrac{S_{\triangle ABD}}{S_{\triangle ADC}}\)的写法也是因为有向面积的概念,我们不再解释:
有向面积:以\(A,B,C\)为逆时针顺序的三角形的面积记为\([A B C]\),顺时针面积为负。