正弦定理系
约 1445 个字 10 张图片 预计阅读时间 7 分钟
共边比例定理
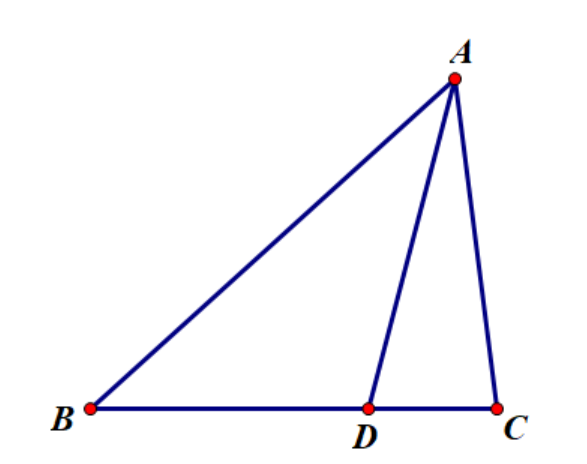
如图,$\triangle ABC$及$BC$边上一点$D$,有$\dfrac{S_{\triangle ABD}}{S_{\triangle ADC}}=\dfrac{BD}{DC}$.
证明见奠基性的正弦定理部分。
分角定理


如图,$\triangle ABC$及$BC$边上一点$D$,有$\dfrac{BD}{DC}=\dfrac{AB\sin\angle BAD}{AC\sin\angle DAC}$.
证明见奠基性的正弦定理部分。
分角定理给出了共线线段比例的一般处理方法,以及"分角"(\(\angle BAC\)及其一条角分线\(AD\)组成的图形)的一种处理方法。由于构型简单,可被广泛使用。
角元塞瓦定理
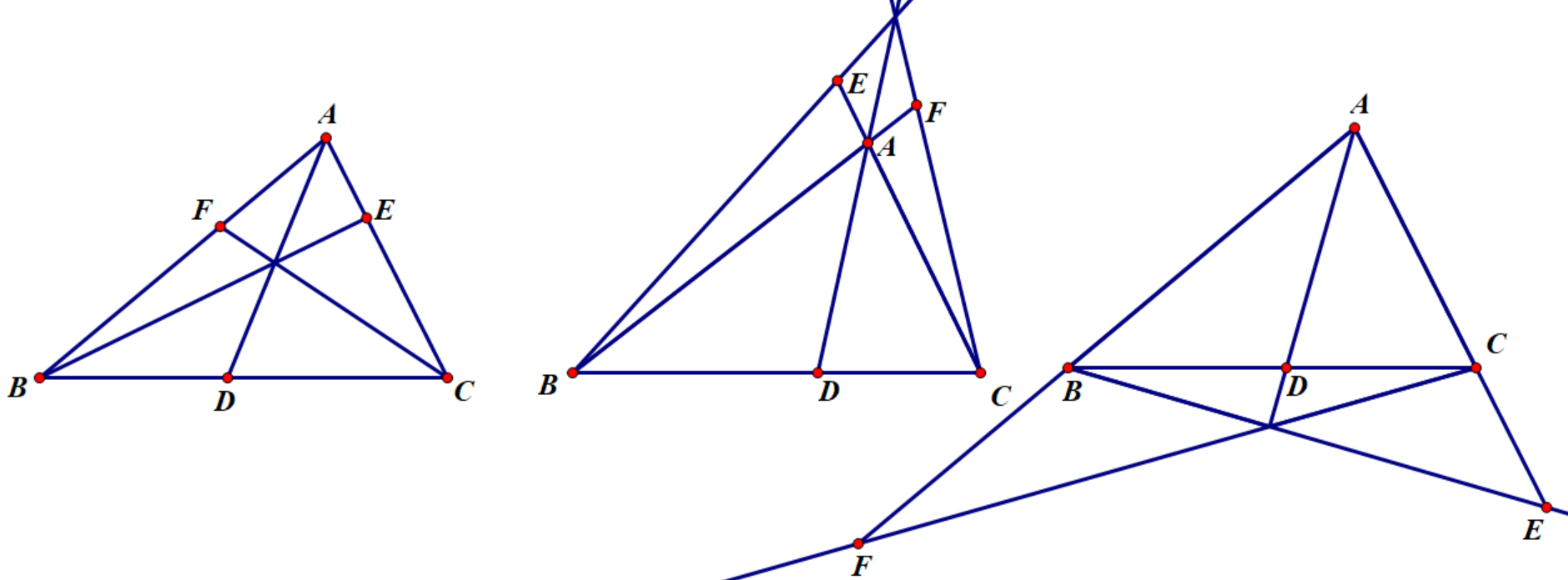
 多种形式的Ceva定理
多种形式的Ceva定理 塞瓦定理:
\(D,E,F\)分别在直线\(AB,BC,CA\)上,则
\(AD,BE,CF\) 三线共点或两两平行 \(\Leftrightarrow\) \(\dfrac{A D}{D B} \cdot \dfrac{B E}{E C} \cdot \dfrac{C F}{F A}=1.\)
定理之证明
必要性:
若三线共点,令共点为P,则\(\dfrac{B D}{D C} \cdot \dfrac{C E}{E A} \cdot \dfrac{A F}{F B}=\dfrac{[ABP]}{[APC]}\cdot\dfrac{[BCP]}{[BPA]}\cdot\dfrac{[CAP]}{[CPB]}=1.\)
若两两平行,用平行线分线段成比例易得.
充分性: 用同一法+必要性的证明即可.
将边的分比用分角定理改为分角,则可得到角元塞瓦定理:
\(D,E,F\)分别在直线\(AB,BC,CA\)上,则
\(A D,B E,C F\) 三线共点或两两平行 \(\Leftrightarrow\) \(\dfrac{\sin \angle B A D}{\sin \angle D A C} \cdot \dfrac{\sin \angle C B E}{\sin \angle E B A} \cdot \dfrac{\sin \angle A C F}{\sin \angle F C B}=1\) .
定理之证明
定理的证明也很简单,应用塞瓦定理+分角定理,将边的分比转换为角的分比+\(\triangle ABC\)三条边的轮换对称比例得证.
角元塞瓦定理的优越性在于,它不关心\(D,E,F\)的位置,以及三条线的共点有什么性质,只关心三个分角的比例。在处理“三线共点或两两平行”这件事上有蒙日定理和角元塞瓦定理两大定理抓手,各司其职:
- 蒙日定理关键在于使共点的直线成为根轴,所以在多圆的情况下会成为首选,但是根轴往往不易被发现,需要发掘甚至构造圆与根轴。
- 角元塞瓦定理则限制更少,只要图中的线性条件更多,角元塞瓦定理会成为一个很不错的抓手点。
下面是一个例子:
角元塞瓦定理的抛瓦
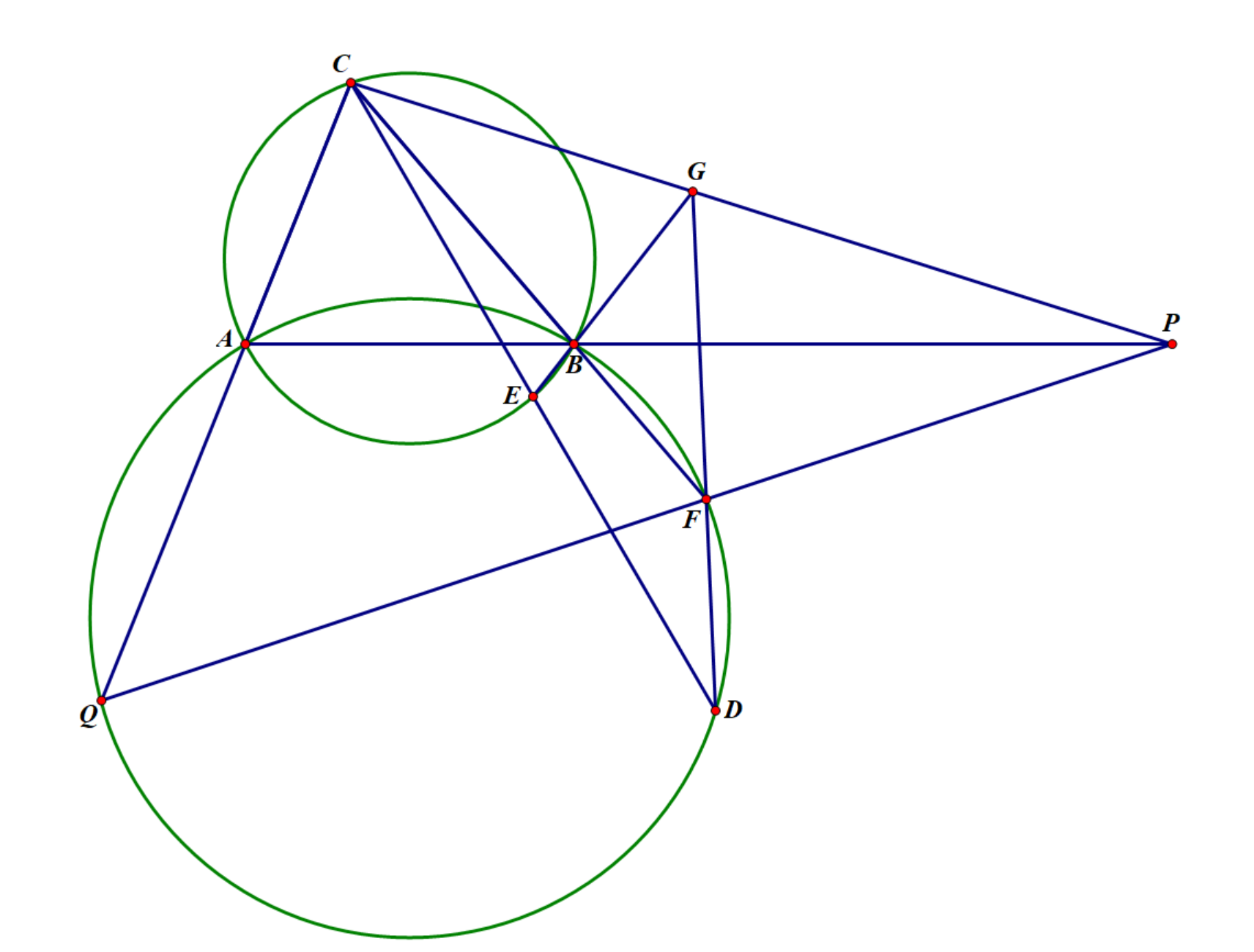
如图,两圆\(\Gamma_1,\Gamma_2\)交于\(A,B\)两点,点\(C,D\)分别在\(\Gamma_1,\Gamma_2\)上且线段\(CD\)与\(\Gamma_1\)的第二个交点为\(E\),直线\(BC\)与\(\Gamma_2\)的第二个交点为\(F\),直线\(DF\)与\(EB\)交于点\(G\),直线\(CG\)与\(AB\)交于点\(P\),求证:若\(E\)为\(CD\)的中点,则直线\(PF\)与\(CA\)的交点\(Q\)在圆\(\Gamma_2\)上。
(2019-3-希望联盟夏令营-P14)
问题之证明
我们设点\(Q\)在圆\(\Gamma_2\)上,反过来证明:\(CG,AB,FQ\)三线共点。
对\(\triangle BFG\)与三条线使用角元塞瓦定理,即
\(\Leftrightarrow\dfrac{\sin\angle DFQ}{\sin\angle QFB}\cdot\dfrac{\sin\angle ABC}{\sin\angle EBA}\cdot\dfrac{\sin\angle BGC}{\sin\angle CGF}=1.\)
由于\(G\)为\(BE\)和\(DF\)的交点,故处理\(\dfrac{\sin\angle BGC}{\sin\angle CGF}\)时需将点\(G\)消掉.
使用分角定理与梅涅劳斯,
\(\dfrac{\sin\angle BGC}{\sin\angle CGF}=\dfrac{BC}{CF}\cdot\dfrac{FG}{BG}=\dfrac{BC}{CF}\cdot\dfrac{DF}{BE}\cdot\dfrac{CE}{DC}.\)
由正弦定理 \(\dfrac{CE}{BE}=\dfrac{\sin\angle EBC}{\sin\angle BCE}\),\(\dfrac{DF}{DC}=\dfrac{\sin\angle FCD}{\sin\angle DFC}\),
\(\dfrac{BC}{CF}=\dfrac{CE}{CD}\cdot\dfrac{\sin\angle CAB\cdot\sin\angle DFC}{\sin\angle EBC\cdot\sin\angle CDF}\)
故\(\dfrac{\sin\angle BGC}{\sin\angle CGF}=\dfrac{CE}{CD}\cdot\dfrac{\sin\angle CAB}{\sin\angle CDF}\),即证:
\(\dfrac{\sin\angle DFQ}{\sin\angle QFB}\cdot\dfrac{\sin\angle ABC}{\sin\angle EBA}\cdot\dfrac{\sin\angle CAB}{\sin\angle CDF}\cdot\dfrac{CE}{CD}=1.\)
经过探索,我们采用基本量表示的方法:
设\(\angle BCD=\alpha\),\(\angle DFQ=\beta\),则导角后即证:
\(\dfrac{\sin\beta}{\sin A}\cdot\dfrac{\sin B}{\sin(C-\alpha)}\cdot\dfrac{\sin A}{\sin(A+\alpha+\beta)}\cdot\dfrac{CE}{CD}=1\).
\(\Leftrightarrow\dfrac{2CE}{CD}\sin B\sin\beta=2\sin(A+\alpha+\beta)\sin(C-\alpha)\\ =\cos(A-C+2\alpha+\beta)-\cos(A+C+\beta)\\ =\cos(A-C+2\alpha+\beta)+\cos B\cos\beta+\sin B \sin\beta\)
由条件,对\(\triangle ADC\)用正弦定理
\(\dfrac{CD}{\sin\beta}=\dfrac{AC}{\sin(\beta+\alpha-C)}=\dfrac{CE\sin B}{\sin(A+\alpha)\sin(\beta+\alpha-C)}.\)
即\(-\dfrac{2CE}{CD}\sin B\sin\beta=2\sin(A+\alpha)\sin(C-\beta-\alpha)\\ =\cos(A-C+2\alpha+\beta)-\cos(A+C-\beta)\\ =\cos(A-C+2\alpha+\beta)+\cos B\cos\beta-\sin B \sin\beta\)
故结论成立 \(\Leftrightarrow 2CE=CD\). 得证.
张角定理


如图,$\triangle ABC$ 及一点 $D$,有:
$B,C,D$ 共线 $\Leftrightarrow \dfrac{\sin\angle BAD}{AC}+\dfrac{\sin\angle DAC}{AB}=\dfrac{\sin\angle BAC}{AD}.$
由于有向角的存在,这个式子已经蕴含 \(D\) 不在线段 \(BC\) 上的情形.
定理之证明
用有向面积:
\(B,C,D\) 共线 \(\Leftrightarrow [ABD]+[ADC]=[ABC]\)
\(\Leftrightarrow AB\cdot AD\sin\angle BAD+AD\cdot AC\sin\angle DAC=AB\cdot AC\sin\angle BAC\)
\(\Leftrightarrow \dfrac{\sin\angle BAD}{AC}+\dfrac{\sin\angle DAC}{AB}=\dfrac{\sin\angle BAC}{AD}.\)
张角定理的强大之处在于它只要有一个点 \(A\) 处的三条线组成的分角和三条线的长度就可以确定共线关系,而不关心 \(B,C,D\) 这样的点在哪里,以及它们之间的关系。
相较于坐标、复数等解共线的方程,三角法解共线会更简单一点,特别是作为分母的三条边长度表达式有较多公因式时,通分会简单很多。
除了共线问题的证明,张角定理也常用来进行分角线长度的计算。