余弦定理系
约 750 个字 6 张图片 预计阅读时间 4 分钟
等差幂线定理
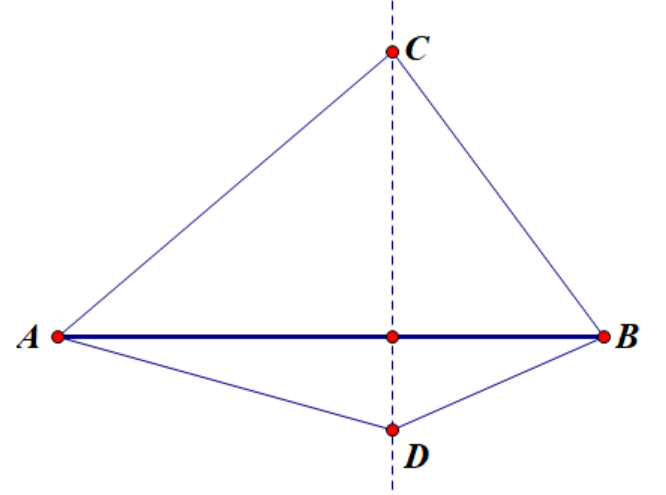
如图,$AB\perp CD\Leftrightarrow AC^2-BC^2=AD^2-CD^2$.
定理之证明
证明是简单的,取出垂足利用勾股定理即可(必要性直接取,充分性对垂足用同一法即可).
除了一般的几何刻画,等差幂线定理在三角证明中也是常有一席之地,特别是在边的平方能被妥善处理时,等差幂线定理会是不错的选择。
斯特瓦尔特定理
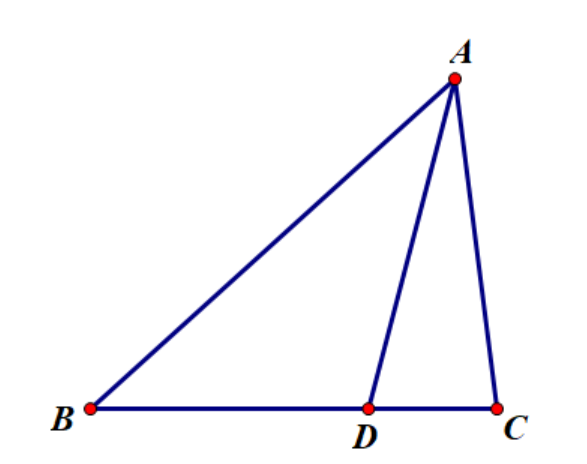
如图,则有$AD^2=AB^2\cdot\dfrac{DC}{BC}+AC^2\cdot\dfrac{BD}{BC}-\overrightarrow{BD}\cdot\overrightarrow{DC}$.
定理之证明
利用向量运算和余弦定理:
\(AD^2=(\overrightarrow{AB}+\overrightarrow{BD})(\overrightarrow{AC}-\overrightarrow{DC})\\ =\overrightarrow{AB}\cdot\overrightarrow{AC}-\overrightarrow{AB}\cdot\overrightarrow{DC}+\overrightarrow{BD}\cdot\overrightarrow{AC}-\overrightarrow{BD}\cdot\overrightarrow{DC}\\ =\dfrac{1}{2}(b^2+c^2-a^2+\dfrac{DC}{BC}(c^2+a^2-b^2)+\dfrac{BD}{BC}(b^2+a^2-c^2))-\overrightarrow{BD}\cdot\overrightarrow{DC}\\ =c^2\cdot\dfrac{DC}{BC}+b^2\cdot\dfrac{BD}{BC}-\overrightarrow{BD}\cdot\overrightarrow{DC}.\)
与张角定理相似,斯特瓦尔特定理也可以(甚至是只能)用来计算分角线长度,但是很明显,二者应用的情形不同:
- 在对边比例已知而分角未知时,斯特瓦尔特定理是更优解
- 而在对边未知而分角已知时,张角定理更合适
托勒密定理
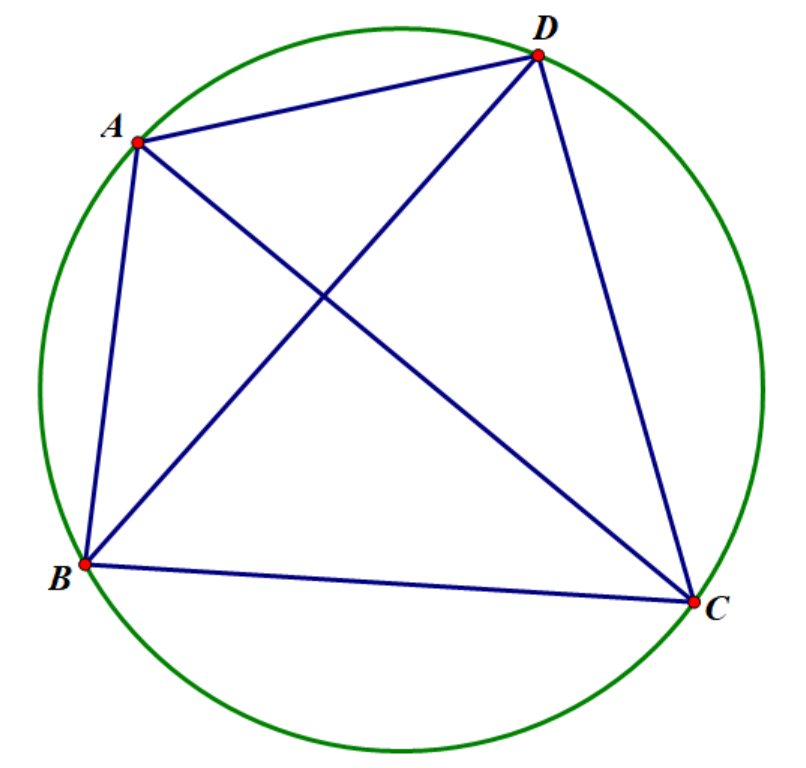

如图,有:
$ABCD$为圆内接四边形 $\Leftrightarrow AB\cdot CD+AD\cdot BC=AC\cdot BD$.
定理之证明
为了化简方便,我们令\(AB=a,BC=b,CD=c,AD=d,AC=e,BD=f\),
则由余弦定理:\(\cos\angle BAD=\dfrac{a^2+d^2-f^2}{2ad}\),\(\cos\angle BCD=\dfrac{b^2+c^2-f^2}{2bc}\),
且由圆内接 \(\cos\angle BAD+\cos\angle BCD=0\),整理得:
\(f^2(ad+bc)=(a^2+d^2)bc+(b^2+c^2)ad\\ =(a^2bc+b^2ad)+(d^2bc+c^2ad)\\ =ab(ac+bd)+cd(ac+bd)=(ab+cd)(ac+bd).\)
同理对\(\angle ABC\)与\(\angle ADC\)可得 \(e^2(ab+cd)=(ad+bc)(ac+bd)\).
两式相乘得 \((ef)^2=(ac+bd)^2\),此即为所证.
托勒密定理使用正弦定理将三条边转为正弦之后即可得到“著名”的三弦定理:
\(A,B,C,D\) 四点共圆 \(\Leftrightarrow AB\sin\angle CAD+AD\sin\angle BAC=AC\sin\angle BAD.\)
补
虽然是由余弦定理推出的托勒密定理的直接推论,但是我认为三弦定理更应该属于“正弦定理系”
——因为余弦定理系全为二次式,而正弦定理系则多为一次式或其次比例式。
与张角定理相似,三弦定理的优越性在于它只要有一个点 \(A\) 处的三条线组成的分角和三条线的长度就可以确定共圆关系,而不关心 \(B,C,D\) 这样的点在哪里,以及它们之间的关系。
更重要的是,它给出了四点共圆的一个简洁且可操作的解析刻画,相较于坐标、向量与复数,三弦定理让三角法解四点共圆问题变得非常有优势,也比纯几何方法更加“不动脑子”——只需要分别审视一下四个点,哪个点适合当作引出三条线的顶点(取决于这个点处的分角与长度是否更好),剩下的交给三角化简即可。