补充性的余弦定理

  • 正弦定理虽强，直角却是其硬伤。(因为\(\sin 90^{\circ}=1\)，使用正弦定理相当于在使用正弦的定义，无法"破局") 。
  • 此外，诸如 SAS 构型下第三边确定的问题，使用正弦定理也会显得捉襟见肘。
  • 其实……
    使用正弦定理 + 余切联合技术确实可以做，但是未免有点过于那啥了。
    不过写一下过程示范一下也不是不行
    对\(\triangle ABC\)，设\(b,c,A\)已知，利用余切联合技术知：
    $$ \frac{\sin(A+B)}{\sin B}=\frac{c}{b}\Rightarrow \cot B=\frac{c-b\cos A}{b\sin A} $$ $$ \Rightarrow \sin B=\sqrt{\frac{1}{1+\cot^2 B}}=\frac{b\sin A}{\sqrt{c^2+b^2-2bc\cos A}} $$ 由正弦定理即得：\(a=\sqrt{b^2+c^2-2bc\cos A}\).
    其实就是把余弦定理推了一遍

    因此有必要引入余弦定理：

    对\(\triangle ABC\)，有： $$ a^2=b^2+c^2-2bc\cos A $$ $$ b^2=c^2+a^2-2ca\cos B $$ $$ c^2=a^2+b^2-2ab\cos C $$
定理之证明

上面已经证过了.jpg

引入向量的内积易证.

我们利用正弦定理和三角函数的基本运算公式：

\(a^2=(b\cos C+c\cos B)^2=b^2(1-\sin^2 C)+c^2(1-\sin^2 B)+2bc\cos B\cos C\)
\(=b^2+c^2-(b\sin C-c\sin B)^2+2bc(\cos B\cos C-\sin B\sin C)\)
\(=b^2+c^2-2bc\cos A\).

该过程具有一般性，轮换对称也成立。得证。

特别的，当某一个内角为 \(90^{\circ}\) 时，余弦定理退化为勾股定理。
(这也是笔者没有写用勾股定理证明余弦定理的原因，就是希望从基础的定义出发推导其他结论，而勾股定理属于二级结论，用它来证明虽然不难，但不太符合笔者的意图。)

有关勾股定理的拓展阅读

关于“\(\sin^2 x+\cos^2 x=1\)”这一命题的独立性，最近似乎有了突破：有两位女高中生证明了基于基本的代数知识，该式可被独立证明，不依赖于勾股定理，并进一步表明，三角学并不是必须依赖于勾股定理才能建立。
见


利用诱导公式可知，只需证明对\(\forall \alpha \in (0,\dfrac{\pi}{4}]\)，\(\sin^2 \alpha+\cos^2\alpha=1\).

命题之证明

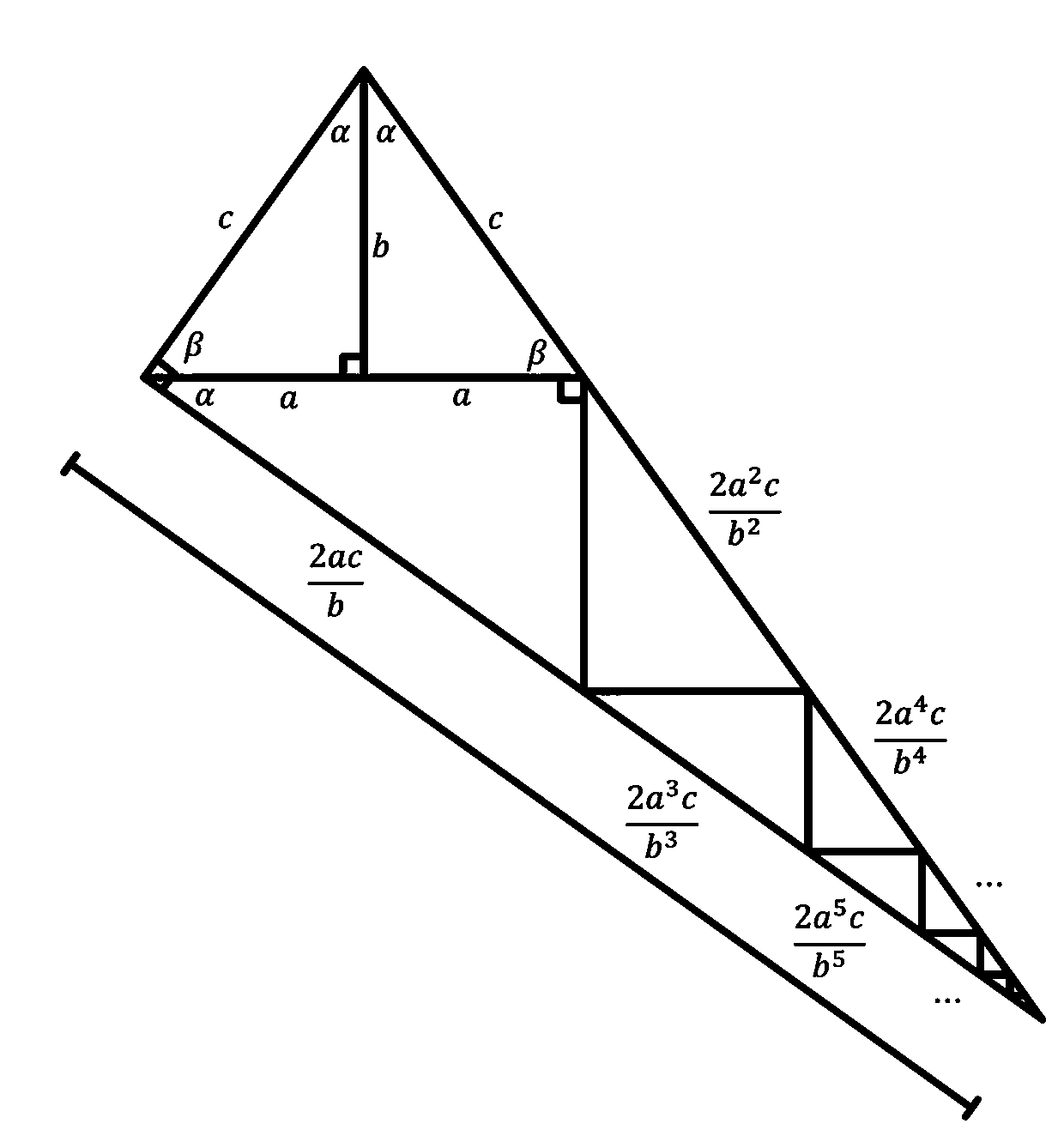
对于非等腰直角三角形，不妨设\(\alpha < \dfrac{\pi}{4}\)构造图形如图，长度关系图中已有。
由级数知 除\(c\)外另一条直角边长\(=\frac{2ac}{b}+\frac{2a^3c}{b^3}+\frac{2a^5c}{b^5}+\cdots\)
\(=\dfrac{2ac}{b}(\displaystyle\sum\limits_{i=0}^{\infty}(\frac{a^2}{b^2})^i)=\frac{2ac}{b}\frac{1}{1-\frac{a^2}{b^2}}=\dfrac{2abc}{b^2-a^2},\)
斜边长\(=c+\frac{2a^2c}{b^2}+\frac{2a^4c}{b^4}+\cdots=c+\frac{2a^2c}{b^2}\frac{1}{1-\frac{a^2}{b^2}}=\dfrac{c(a^2+b^2)}{b^2-a^2}.\)

故\(\sin 2\alpha=\dfrac{2ab}{a^2+b^2},\cos 2\alpha=\dfrac{b^2-a^2}{a^2+b^2}\)，

易验证此时 \(\sin^22\alpha+\cos^22\alpha=1\).

\(\alpha=\dfrac{\pi}{4}\) 时向等腰直角三角形的斜边作高线，用射影定理得\(2\sin^2 \dfrac{\pi}{4}=1\)，即\(\sin^2\dfrac{\pi}{4}+\cos^2\dfrac{\pi}{4}=1\).

综上：原命题成立。得证。
\(\Box\)

余弦定理最大的好处就是它能够比较好地处理正弦定理不能直接处理的问题。

  • SAS构型：事实上SAS构型有两种处理方式：
    • 利用余切联合技术求两条已知边所对角的余切.
    • 利用余弦定理求已知角的对边.
  • 后者用余弦定理处理会非常轻松(只不过由于引进了平方项，要注意幂次的处理balabala).
  • 垂直相关：利用勾股定理可以推导出与垂直密切相关的定理：等差幂线定理，在处理垂直方面具有较为广泛的应用。
  • 分角线的长度：虽然张角定理可以给出分角线的长度，但若分角具体大小未知，使用分角定理就会面临一定的困难。这个时候使用余弦定理推导出的斯特瓦尔特定理就能解决一部分情况。 ……

总而言之，余弦定理能够不错地补充正弦定理所涉及不到的部分，与正弦定理一起构筑好了三角学平面几何定理的基石。