塞瓦型补充
约 950 个字 6 张图片 预计阅读时间 5 分钟
在解决几何问题的过程中,有一个较为常见的构型:
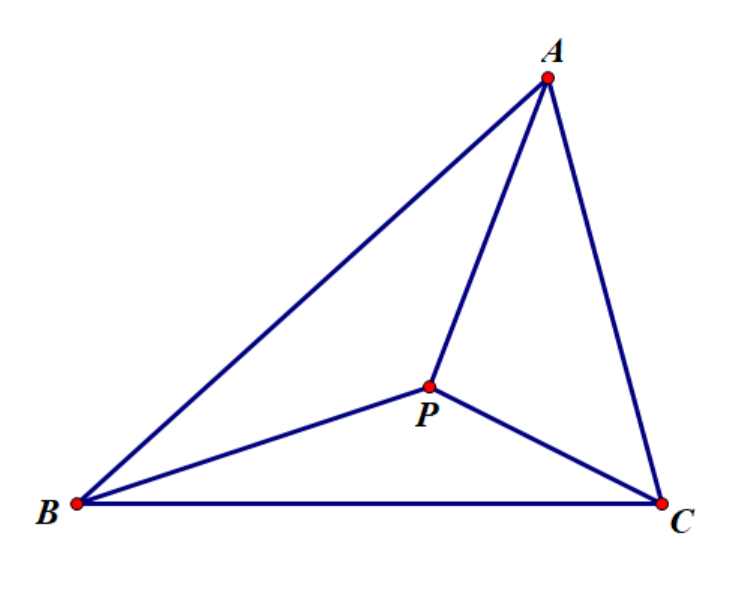
 塞瓦型
塞瓦型 \(P\)为\(\triangle A B C\)内一点,考察\(P A \cdot B C\)的性质。
由于这是一个二次式,而正弦定理是一次式,塞瓦定理、梅涅劳斯定理是齐次式,而与二次相关的直接结论便是余弦定理,但余弦定理的交叉项需要两条边共顶点,图中的这两条边\(P A\)与\(B C\)显然不满足这一点,所以已有的定理无法直接处理这个问题。
这时就需要如下引理:
(Ceva型引理)图如上,则有: $$ \dfrac{P A \cdot B C}{\sin(\angle B P C-\angle B A C)}=\dfrac{P B \cdot A C}{\sin(\angle A P C-\angle A B C)}=\dfrac{P C \cdot A B}{\sin(\angle A P B-\angle A C B)} $$
引理之证明
构造相似形如下:
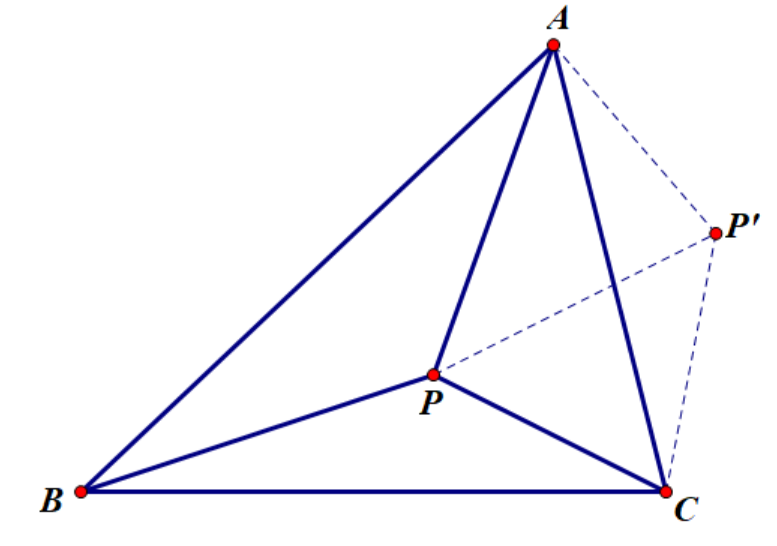
且 \(\angle P C P'=\angle A B P+\angle A C P=\angle B P C-\angle B A C\), \(\angle C P P'=\angle A P C-\angle A B C\), 故有: $$ P A \cdot B C=A B \cdot \dfrac{P C \sin(\angle B P C-\angle B A C)}{\sin(\angle A P C-\angle A B C)} $$ 即 $$ \dfrac{P A \cdot B C}{\sin(\angle B P C-\angle B A C)}=\dfrac{P C \cdot A B}{\sin(\angle A P B-\angle A C B)} $$ 同理有其他两式。结论得证。
值得一提的是
此引理是笔者遇到的印象十分深刻的引理,在某些情况下有化腐朽为神奇之用
下面用一个例子展示一下这个引理的强大之处:
$\space$
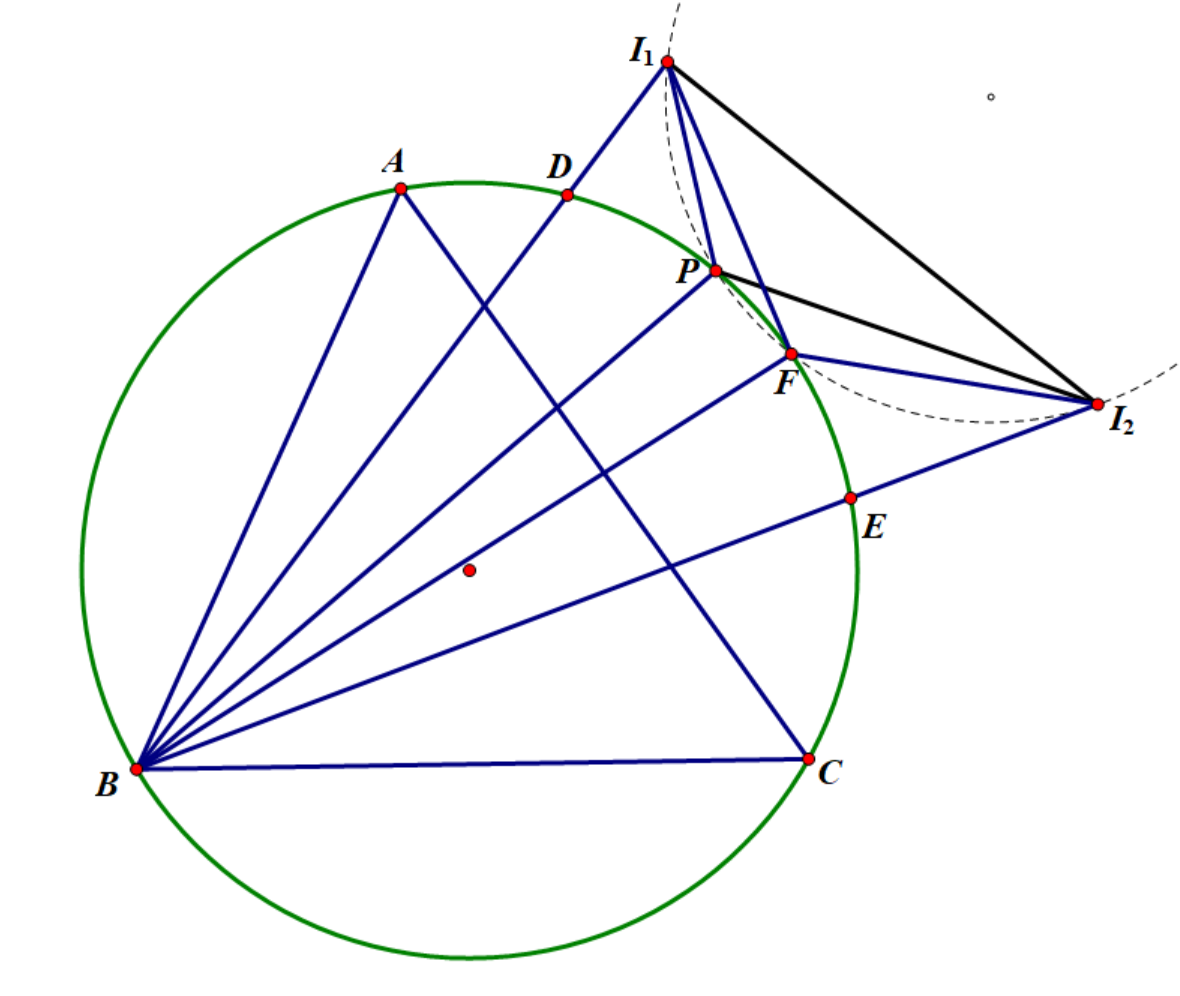
P为$\triangle A B C$外接圆上一动点,$I_1$和$I_2$为$\triangle A B P$和$\triangle B C P$的旁心,证明:$\triangle I_1 I_2 P$的外接圆过不依赖于$P$的定点。
定理之证明
证明:设\(\triangle A B C\)的外接圆为\(\omega\),令\(\odot I_1 P I_2 \cap \omega\) 于\(F\),我们证明 \(F\) 即为所求. 设\(B I_1\)交\(\omega\)于\(D\),\(C I_2\)交\(\omega\)于\(E\),记\(\angle B A D=\alpha\),\(\angle F A D=\beta\),利用旁心导角有: $$ \angle A I_1 P=\dfrac{\angle A X P}{2}=\dfrac{B+\angle C A P}{2}=\dfrac{A+B-2 \alpha}{2}=\dfrac{\pi-C}{2}-\alpha, $$ $$ \angle I_1 A P=\alpha \Rightarrow\angle A P I_1=\dfrac{\pi+C}{2} $$ 同理:$$ \angle A P I_2=\dfrac{\pi+B}{2} , \angle I_1 P I_2=\dfrac{\pi+A}{2} $$ $$ \angle I_1 I_2 F=\angle I_1 P F=\angle A F P-\angle I_1 A F-\angle A I_1 P=\angle A I_1 P-\angle I_1 A F=\dfrac{\pi-C}{2}-\alpha-\beta $$ $$ \angle I_2 I_1 F=\pi-\angle I_1 I_2 F-\angle I_1 P I_2=\dfrac{C-A}{2}+\alpha +\beta, \angle I_2 A F=\dfrac{A}{2}-\beta. $$ 从而 $$ \angle I_1 I_2 F+\angle I_1 A F=\dfrac{\pi-C}{2}-\alpha, \angle I_2 I_1 F+\angle I_2 A F=\dfrac{C}{2}+\alpha. $$ 由引理: $$ \dfrac{I_1 F \cdot A I_2}{\sin(\dfrac{\pi-C}{2}-\alpha)}=\dfrac{I_2 F \cdot A I_1}{\sin(\dfrac{C}{2}+\alpha)} $$ $$ \Rightarrow \dfrac{I_1 F}{I_2 F}=\dfrac{A I_1}{A I_2} \cdot \dfrac{\cos(\dfrac{C}{2}+\alpha)}{\sin(\dfrac{C}{2}+\alpha)}. $$ 而由内心性质 $$ A I_1=4R \cos \dfrac{\angle A B P}{2} \cos \dfrac{\angle A P B}{2}=4R \cos \frac{\pi-C-2\alpha}{2} \cos \dfrac{C}{2}=4R \sin (\dfrac{C}{2}+\alpha) \cos \dfrac{C}{2}, $$ $$ A I_2=4R \cos \dfrac{\angle A C P}{2} \cos \dfrac{\angle A P C}{2}=4R \cos (\dfrac{C}{2}+\alpha) \cos \dfrac{B}{2}, $$ $$ \Rightarrow \dfrac{I_1 F}{I_2 F}=\dfrac{\sin \angle I_1 I_2 F}{\sin \angle I_2 I_1 F}=\dfrac{\cos(\dfrac{C}{2}+\alpha+\beta)}{\sin(\dfrac{C-A}{2}+\alpha+\beta)}=\dfrac{\cos(\dfrac{C}{2}+\angle B A F)}{\sin(\dfrac{C-A}{2}+\angle B A F)}=\dfrac{\cos \dfrac{C}{2}}{\cos \dfrac{B}{2}} $$ 由余切联合定理知\(\tan \angle B A F\)为只依赖于\(A,B,C\)的值,所以\(F\)为定点,得证.